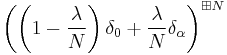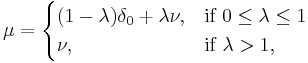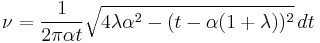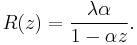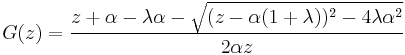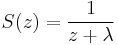Free Poisson distribution
In the mathematics of free probability theory, the free Poisson distribution is a counterpart of the Poisson distribution in conventional probability theory.
Definition.[1] The free Poisson distribution with jump size  and rate
and rate  arises in free probability theory as the limit of repeated free convolution
arises in free probability theory as the limit of repeated free convolution
as N → ∞.
In other words, let 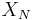 be random variables so that
be random variables so that 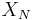 has value
has value  with probability
with probability 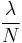 and value 0 with the remaining probability. Assume also that the family
and value 0 with the remaining probability. Assume also that the family 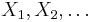 are freely independent. Then the limit as
are freely independent. Then the limit as 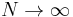 of the law of
of the law of  is given by the Free Poisson law with parameters
is given by the Free Poisson law with parameters 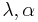 .
.
This definition is analogous to one of the ways in which the classical Poisson distribution is obtained from a (classical) Poisson process.
The measure associated to the free Poisson law is given by
where
and has support ![\alpha (1-\sqrt{\lambda})^2,\alpha (1%2B\sqrt{\lambda})^2]](/2012-wikipedia_en_all_nopic_01_2012/I/63e7196d6f0f56c3471fa8a4987343e6.png) .
.
This law also arises in random matrix theory as the Marchenko–Pastur law. Its free cumulants are all equal to  .
.
Some transforms of this law
We give values of some important transforms of the free Poisson law; the computation can be found in e.g. in the book Lectures on the Combinatorics of Free Probability by A. Nica and R. Speicher[2]
The R-transform of the free Poisson law is given by
The Stieltjes transformation (also known as the Cauchy transform) is given by
The S-transform is given by
in the case that 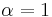 .
.